3.7 Exercises
1. 표 3.4에 주어진 p-값이 대응되는 귀무가설을 설명하여라. 이 p-값들을 바탕으로 어떤 결론을 내릴 수 있는지 설명하여라. 당신의 설명은 선형모델의 계수가 아닌 판매, TV, 라디오, 신문 등의 용어로 표현되어야 한다.

t통계를 사용했기 때문에 H0, 귀무가설은 각각의 변수들과 광고 예산간의 관계를 알아본 것이다.
그렇기 때문에 각각의 회귀 계수는 Bi 0이다라는 귀무가설이 세워진다.
그리고 위의 표를 보면, 유의확률 p-value가 유의수준 0.05, 0.01보다 훨 큰 값은 newspaper 밖에 없기 때문에 newspaper는 귀무가설을 기각하지 못하고 회귀계수가 0이되며, 나머지는 회귀계수가 Coefficient를 따라간다.
결국은 신문 광고는 광고 예산을 늘려도 의미가 없다고 생각하면 된다.
2. KNN 분류와 KNN 회귀 방법의 차이점을 설명하시오.
KNN 분류는 범주형 변수 분류에 사용되고, KNN 회귀는 연속형 변수의 예측에 사용된다.
3. X1 = GPA, X2 = IQ, X3 = Level (1은 대학 0은 고등학교), X4 = GPA와 IQ의 관계, X5 = GPA와 Level의 관계
response는 졸업 후 초봉(단위 : 천달러)이다. 모형 적합을 위해 최소제곱을 사용했고,
βˆ0 = 50, βˆ1 = 20, βˆ2 = 0.07, βˆ3 = 35, βˆ4 = 0.01, βˆ5 = −10를 얻었다.
a) 어떤 설명이 맞나?
1) (IQ와 GPA는 고정)고등학교 졸업생은 대학 졸업생보다 평균적으로 많이 번다.
salary = 50 + 20(GPA) + 0.07(IQ) + 35(level) + 0.01(GPA * IQ) -10(GPA * level)이다.
여기서 고등학교 졸업 (level = 0)이라고 하면, salary = 50 + 20(GPA) + 0.07(IQ) + 0.01(GPA * IQ)의 식이 나오고,
대학교 졸업 (level = 1) 이라고 하면, salary = 50 + 20(GPA) + 0.07(IQ) + 35 + 0.01(GPA * IQ) -10(GPA)의 식이 나온다.
따라서 대학교 졸업생이 35 - 10GPA 만큼의 연봉이 높다. (GPA는 고정이기 때문에 35가 높다는 것을 알 수 있다)
2) IQ와 GPA 값이 고정된 경우, 평균적으로 대학 졸업생이 고등학교 졸업생보다 높은 월급을 받습니다.
3) IQ와 GPA 값이 고정되고, GPA가 충분히 높다는 것을 전제로 할때, 고등학고 졸업생은 대학 졸업생들보다 평균적으로 더 많은 돈을 번다.
GPA가 3.5보다 클 경우 고등학교 졸업생은 평균적으로 대학 졸업생보다 더 높은 월급을 받게 됩니다.
4) IQ와 GPA 값이 고정되고, GPA가 충분히 높다는 것을 전제로 할때, 대학 졸업생은 고등학교 졸업생들보다 평균적으로 더 많은 돈을 번다.
(b) IQ가 110이고, GPA가 4.0인 대졸자의 급여를 예측하라.
salary = 50 + 20(GPA) + 0.07(IQ) + 35 + 0.01(GPA * IQ) -10(GPA) (대졸자의 경우)이므로
50 + 80 + 0.07 * 110 + 35.+ 0.01(4 * 110) - 10*4 = 137.1이다.
(c) GPA/IQ 상호작용 계수가 매우 작기 때문에, 상호작용 효과에 대한 증거가 거의 없다..?
상호작용 계수로 상호작용의 유무나 중요성을 결정할 수 없다.
4. 단일 예측 변수와 정량적 반응을 포함하는 관측치의 수 (n) = 100, 선형 모델에 적합시킬 예정
Y = β0 +β1^X +β2X^2 +β3X^3 +ε.(세제곱 회귀 모델) vs Y = β0 +β1X +β2X2 +β3X3 +ε. (선형회귀)
a) X와 Y 사이의 관계가 선형이라고 하면,
training residual sum of squares (RSS) for the linear regression
vs
training RSS for the cubic regression
당연하게도 더 유연하게 모델에 적합될 수 있는 the cubic regression의 RSS가 더 작을 것이다.
b) test에서는 cubic regression은 과적합의 문제가 있기 때문에 성능은 선형이 더 좋을 수 있다.
c) 비선형이라면 linear regression vs cubic regression?
당연하게도 비선형이면 cubic regression이 더 좋을 것이다.
d) test에서도 cubic regression이 더 좋을 확률이 크지만, 만약에 약한 비선형 관계라면 과적합 문제로 인해 linear regression 더 성능이 좋을 것이다.
5. 절편이 없이 선형회귀로 학습시킨 모델이 있는데,

이게 뭘까..? 예측한 직선 위의 점들인거 같은데? 예측한 직선위의 점들이면 a1.... an이 의미가 있는가? 수식적으로 해석이..
예측한 원점을 지나는 하나의 직선이 특정 점들의 합으로 이뤄진다. 근데 그 점들은 실제 y값들에 각 a들을 곱해서 더하는 값이다..
그냥 직선 위에 있는 갑들이라 B의 미세값들 아닌가?
6. (3.4)를 사용하여 단순 선형 회귀 분석의 경우 최소 제곱선이 항상 X와 Y의 평균값을 통과하는 것을 설명하시오.

단순 선형 회귀

이런식으로 증명 가능한 것 같은데... 이게 맞나 싶다.
추가로

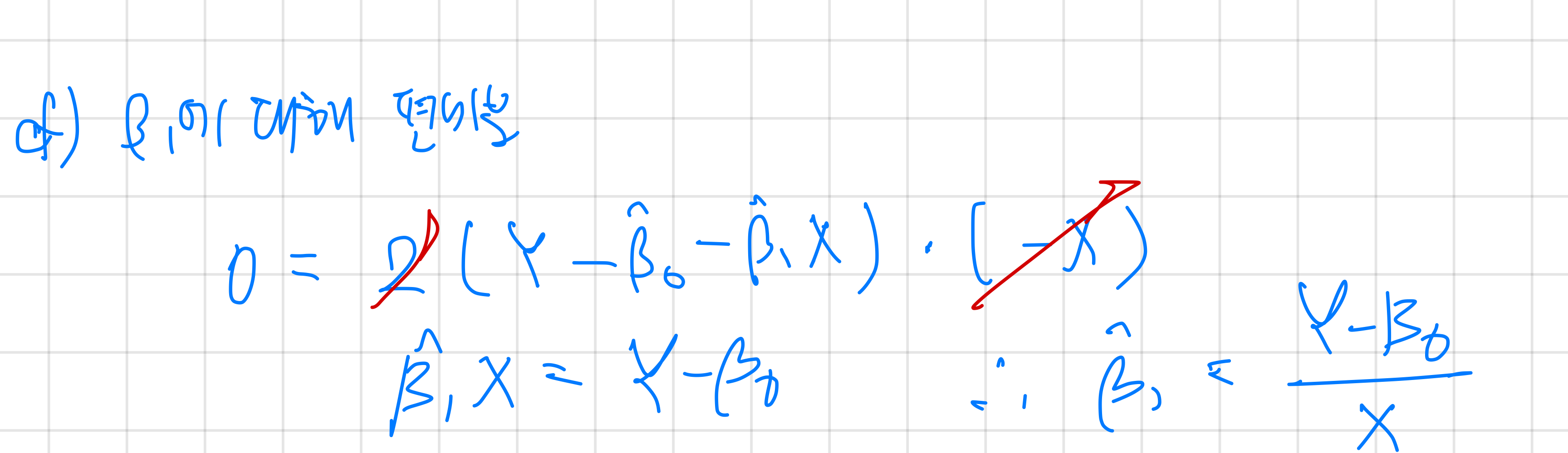
저번부터 궁금했던거를 정리해봤다. 아직 이해가 안가.. 예 이해가 값니다!
7. 단순 선형회귀 하는 경우 위의 식에서 3번이 참이라고 하는데, 이걸 증명하라..
공분산은 두 변수가 함께 어떻게 움직이는지를 나타내는 척도입니다. 즉, X의 한 단위 변화가 Y에 미치는 평균적인 영향을 나타냅니다. 분산은 변수의 변동성을 나타내는 척도입니다. 뭐 수식으로 증명하라고? 난 못해..
'미래내일일경험 - 빅리더(23.06~23.12) > 교육' 카테고리의 다른 글
| [스터디챌린지] ICT융합대학 스터디 챌린지 8주차(8/19 ~ 8/25) (0) | 2023.08.25 |
|---|---|
| [스터디챌린지] ICT융합대학 스터디 챌린지 7주차(8/12 ~ 8/18) (0) | 2023.08.18 |
| [스터디챌린지] ICT융합대학 스터디 챌린지 6주차(8/05 ~ 8/11) (1) | 2023.08.11 |
| [An Introduction to Statistical Learning] 3. Linear Regression (0) | 2023.08.08 |
| [스터디챌린지] ICT융합대학 스터디 챌린지 5주차(7/29 ~ 8/04) (0) | 2023.08.04 |