목차
3. Linear Regression
3.1 Simple Linear Regression
3.1.1 Estimating the Coefficients
3.1.2 Assessing the Accuracy of the Coefficient Estimates
3.1.3 Assessing the Accuracy of the Model
3.2 Multiple Linear Regression
3.2.1 Estimating the Regression Coefficients
3.2.2 Some Important Questions
3.3 Other Considerations in the Regression Model
3.3.1 Qualitative Predictors
3.3.2 Extensions of the Linear Model
3.3.3 Potential Problems
3.4 The Marketing Plan
3.5 Comparison of Linear Regression with K-Nearest Neighbors
이 책에서는 예시를 광고 플랫폼 ( TV, 라디오 그리고 신문)과 광고의 효과, 광고 예산과 광고의 효과로 들고 있다.
(2장에서 보여준 데이터셋이다) 3장을 시작할 때, 데이터에 기반해서
1. 광고 예산과 판매량의 상관관계
2. 얼마나(How strong) 그 둘의 사이가 관계 있는지
3. (광고의 플랫폼) 미디어와 판매량이 관계가 있는지
4. 그 둘의 사이가 얼마나 상관관계가 있는지
5. 미래 판매 예측량을 얼마인지
6. 이게 선형관계인지?
7. 미디어 광고 간의 시너지가 있는지
이 질문들을 모두 linear regression을 진행하면 답할 수 있다고 이야기한다.
선형회귀는 매우 간단한 지도 학습 방법 중 하나이다. 말 그대로 "선형" 방정식으로 모델을 만들기 때문에 한계가 명확하다.
3.1 Simple Linear Regression (선형 회귀 분석)
하나의 변수와 다른 하나의 변수의 상관관계를 나타내는 식으로 표현되는 관계이다.

와 같이 수식으로 표현되며, 위의 예시로 생각하면

과 같이 생각될 수 있다. 말 그대로 근삿값이다. 관측값(observation)들을 단순한 직선으로 모두 나타낼 수 없기 때문에 근사 값으로 나타낸다. 근사 값으로 식을 풀어가기에는 사실 무리가 있다. 단순하게 근사한 식인데?라고 제시하는 것보다는 우리가 예측한 식과 정확도를 같이 제시해 주는 것이 좋다.

그래서 우리는 예측값으로 식을 나타낸다 ( 예측값은 모자를 쓰고 있다)
그런데 여기서 우리는 B0와 B1 값은 알려진 것이 없다. 그러면 우리는 관측값들로부터 추청 해야 한다.

n개의 관측값들이 주어졌을 때, 이 값들로 B0와 B1 값을 추정한다.

저 수많은 빨간 점들이 observation라고 하자. 우리는 이 점들을 표현할 수 있는 직선을 하나 그을 것이다. 그러면 어떤 직선이 가장 좋을까?
당연하게도 예측값과 실제값이 차이가 가장 작은 직선이 좋을 것이다. 근데 한 점에 대해서만 직선을 그을 수 없으니, 모든 점에 대해서 예측값과 실제값의 차이가 적은 직선을 긋는다.
우리는 예측값과 실제값의 차이 즉,

를 최소화하는 친구를 찾아야 한다. 우리는 이것을 residual : 잔차라고 하며 잔차 제곱의 합(RSS : residual sum of squares)을 최소화하는 (모든 점들에 대해서 잔차를 최소화해야 하므로 합을 구해서 계산하며, 잔차는 양수도 음수도 있기 때문에 제곱을 해서 더한다.)


위에서 이야기한 것처럼 실제값에서 예측값을 빼주고 제곱을 해서 모두 더한다. 우리는 이것을 최소화하는 방향으로 직선을 그을 것이다.
그래서 RSS를 최소화하는 방향으로 B0와 B1을 결정하는 것이다.

뭐 수식은 이와 같은데, 크게 의미 없다. 우리가 정할 것이 아니라 모델이 만들어준다. 굳이 기억은 하지 말자 뇌 용량 아깝다.
3.1.2 Assessing the Accuracy of the Coefficient Estimates (계수 추정의 정확성 평가)

X와 Y 사이의 실제 관계는 위의 관계처럼 알려지지 않은 함수 f에 대해 Y = f(x) + ε의 형태를 취한다고 가정하고, 여기서 ε는 mean-zero random error 항입니다. f(x)가 일차함수에 근사화되면, 우리는

여기서 B0는 X = 0 일 때 Y의 기댓값(y절편)이고, B1은 기울기다. (X가 1 증가할 때 Y는 B1 증가한다.)
일차함순데 ε는 왜 들어가냐고 물어보면 이건 우리의 식으로 설명이 안 되는 친구이므로 따로 빼놓는 것이다.
3.5의 모형은 말 그대로 the population regression line, 한국어로 하면 모집단 회귀선이다.

위의 그래프는 하나의 예시입니다. 빨간 선은 모집단 회귀선, 그니까 실제 데이터고, 파란색 선은 오차 제곱 합이 최소화되는 직선입니다. 왜 완전히 같지 않냐고 물어보면, 이건 그냥 하나의 예측기법일 뿐입니다.
그냥 파란 선도 하나의 예측한 직선일 뿐입니다. 여러 샘플 데이터들이 나오면 파란 선은 여러 개가 될 수 있습니다.
책에서는 모평균을 추정할 때와 여기서의 직선을 예측할 때랑 다른 게 없다,라는 식으로 이야기합니다. (이해한 게 맞나 싶네요)
그니까 실제값보다 조금 더 크게 예측할 수도 있고, 실제 값보다 더 작게 예측할 수 도 있다고 이야기합니다. 그래서 모집단의 평균을 예측하는 것도 마찬가지였으니,

이런 식으로 이야기하던 표준 오차를 아래 수식과 같이 선형회귀 식에 적용할 수 있다고 이야기합니다.

예측한 절편과 예측한 기울기의 표준 오차를 보여주는 식이다. 이때, 관측치에 대한 오차 e가 일반적인 분산 (σ^2 = Var(ε))을 따르고 서로 독립이라는 가정이 필요하다.
B1의 편차는 x1이 멀리 퍼져있으면 작아잔고, 편차가 n에 따라 어떻게 감소하는지 알려준다.
그리고 보통은 σ^2 알려져 있지 않지만 data를 통해 추정할 수 있다.
이 σ의 추정치는 잔차 표준 오차(RSE) residual standard error로 알려져 있고,

와 같은 식으로 알려져 있다.
B1, B0의 95% 신뢰 구간은 (보통 Z = 1.96이면 95% 추정구간으로 잡는데 여기서는 2로 잡았다)


여기도 신뢰구간은 normalize의 신뢰구간을 구하는 것과 같아서 간단하게 넘어가겠다.
2. 가설을 세우고 검정을 하기 위해서

(당연하게도 귀무가설을 기각하지 못하면 선형식이 아니게 되는데, 그 말인즉슨 X와 Y가 서로 관계가 없다는 것을 의미한다.)

t검정을 하는데, (one-sample t-test이기 때문에)
만약 X와 Y 사이에 실제로 아무런 관계가 없다면, 우리는 (3.14)가 n - 2 자유도를 갖는 t-분포를 가질 것이라고 예상한다.
( t-분포는 종 모양을 가지며, n이 대략 30보다 큰 값의 경우 그것은 표준 정규분포와 상당히 유사하다. 간단하게 표본의 개수가 작은 정규분포를 따르는 것처럼 보이는 친구라고 생각하면 좋다.)
3.1.3 Assessing the Accuracy of the Model (모델의 적합성 평가)
여기부터는 이미 귀무가설을 기각하고 대립가설을 채택한 경우, 즉 X와 Y의 상관관계가 있다고 나온 경우를 가정한다.
우리는 회귀 모델이 유의하다는 가정하에 얼마나 잘 적합하는지를 R^2 계수와 RSE(the residual standard error)

이런 식으로 보이는데 조금 있다가 자세하게 보겠지만 간단하게 설명하자면,
R^2 (결정계수) : 회귀식의 적합도를 재는 척도이며, 0 ~ 1 사이의 값을 가진다. 상관계수의 제곱 값이며 1일 때 성능이 좋다는 것을 이야기한다.
RSE (잔차 표준 오차) : 이 모델에서 σ의 추정치로 알려져 있고
F - statistic : 모델의 유의성을 이야기한다. (정확한 "F- 검정"은 주로 모형이 최소 제곱을 사용하여 데이터에 적합할 때 발생한다. 연속 확률 분포로, F 검정(F 테스트)과 ANOVA 등에서 주로 사용된다. Fisher)
F-통계량을 사용한 검정에서 귀무가설은 "모든 회귀 계수가 0이다(즉, 독립 변수들이 종속 변수를 예측하는 데 유의미한 영향을 미치지 않는다)"입니다. 대립 가설은 "적어도 하나의 회귀 계수가 0이 아니다(즉, 적어도 하나의 독립 변수가 종속 변수를 예측하는 데 유의미한 영향을 미친다)"입니다.
1. Residual Standard Error (an absolute measure of lack of fit of the model (3.5) to the data.)

오차가 생기는 이유는 당연하게도 완벽한 추론은 없기 때문이다. RSE가 크면 선형회귀 모델의 적합도가 부족하다는 결론을 내릴 수 있다.
(이게 분산의 추정량이라고 이야기되는 것을 보니까 내가 예측한 선형회귀 선에서 얼마나 데이터들이 떨어져 있나를 나타내는 것과 같다. 식을 해석하면 당연한 이야기다 따라서 RSE가 크면 내가 그은 직선에 대해 실제 값들이 많이 떨어져(분산이 큰) 있는 것이다.
2. R^2 통계량 (결정 계수)
이게 위의 표를 RSE 보면 3.26이다. 책에서는 14,000 중에 3,260이 어쩌고 23%가 어쩌고 이해를 못 했다. 왜냐? 추정된 Y값으로 나오기 때문에 단위에 따라 값이 천차만별이다. 그래서 우리는 대체품으로 결정 계수를 사용한다.


이런 식으로 나오는 값이며 보다시피 비율의 형태이기 때문에, Y의 단위와 무방하다는 점 때문에 사용한다.
3.2 Multiple Linear Regression (다중 선형 회귀)
당연하게도 (현실의 많은 데이터들은.. 사실 거의 모든 데이터라고 해도 될 것 같다.) 하나의 값만 Y에 영향을 미치지 않는다. 그래서 다중 선형회귀를 사용한다.

우리 책의 예시만 봐도 판매량은 신문, 라디오, 심지어 티브이나 다른 것들에게도 연관이 된다. 그래서 우리는 이런 식으로

식을 나타낸다.
간단하게 생각하면 선형 회귀 분석이 여러 개 합쳐진 것으로 생각해도 되는 모델이다. 문제는 간단하지 않다는 거
3.2.1 Estimating the Regression Coefficients (회귀 계수의 추정)
단순 선형회귀와 똑같다. 당연하게도 위 3.19 식의 B0... Bp의 값은 알 수가 없다. 그래서 우리는 추정을 해야 하고 거기서 발생하는 잔차들을 모아서 제곱해서 위와 같이 RSS(residuals sum of squared, 잔차제곱합)을 구한다.


이걸 손으로 계산하는 미련한 사람이 당연히 없겠지..? 파이썬이나 R을 사용해서 데이터를 입력해서 나온 값을 "해석을 위한 공부"를 하자.

변수가 2개만 있어도 3차원이 된다. 나중에 차원 개념은 PCA 정도에서, 아니 ML 초반만 가도 나온다. 차원 개념은 column과 비슷한 개념으로 일단 알아두고 넘어가자.

예시로 간단하게 살펴보면, Intercept가 B0라고 보면 되고, 단순하게 Coefficient값만으로 회귀 식(모형)을 만들면
sales = 2.939 + 0.046TV + 0.189 radio - 0.001 newspaper 정도의 식이 나온다.
그런데 p-value를 보자 Intercept와 TV, radio는 모두 0.001보다 작으므로 귀무가설을 기각하고 대립가설을 수용했지만, newspaper는 H0가 True라고 할 때 분포에 있을 확률 (p-value)가 0.85 즉, 85%나 된다. 이를 통해 newspaper를 회귀식에 집어넣는 것은 문제가 있다는 판단을 할 수 있다.

그런데, 위에서 봤던 신문의 단순 선형 회귀식과 많이 달라진 것을 볼 수 있다. 왜일까? 조금만 고민해 보자.
정답은 바로,

우리가 X로 뒀던 독립(예측) 변수들끼리 서로 연관이 있다. 이게 영어로 복잡하게 설명되어 있어서 이해가 어려웠는데 (필자는 다중공선성 인가를 생각했지만, 우리 Gpt선생이 요약해 준 바에 따르면)
우리가 라디오, 텔레비전, 신문에 광고를 하면 판매량이 올라가는 걸 알아봤어요. 그런데 각각 얼마나 효과가 있는지는 까다로운 문제인데, 이를 알아보기 위해 이것들이 판매에 얼마나 영향을 미치는지 살펴봤어요.
첫 번째로, 라디오 광고에 돈을 더 투자하면 판매량이 많이 올라갔어요. 그런데 신문 광고는 처음에는 판매에 영향을 미치는 것처럼 보였어요. 그러나 다른 광고들과 함께 고려하면 신문 광고는 사실 판매에 별로 영향을 주지 않는다는 것을 알 수 있었어요.
왜 그럴까요? 그 이유는, 신문에 많이 광고를 한 곳은 보통 라디오에도 많이 광고를 한다는 것을 알게 되었기 때문이에요. 그래서 신문 광고가 판매량을 높이는 것처럼 보이지만, 실제로는 라디오 광고 때문에 판매량이 높아진 거라는 거죠. 결국, 신문 광고는 라디오 광고의 효과를 대신해서 받아가는 것 같아요.
이런 방식으로 우리는 라디오, 텔레비전, 신문 광고가 판매량에 얼마나 영향을 미치는지 알아보는 것이 중요해요. 이렇게 알면 어디에 광고를 해야 가장 효과적인지 알 수 있거든요.
그러니까 그냥 라디오에 광고를 많이 하면 신문에 광고든 어느 정도 하는데, 라디오 광고 때문에 올라간 판매량이 (신문 광고와 라디오 광고는 어느 정도, 여기서는 35%만큼 연관이 있기 때문에) 단순 선형회귀를 할 때 보이는 신문의 양의 상관성이 다중 선형회귀를 할 때는 의미가 없어 보인다는 것을 이야기한다.
3.2.2 Some Important Questions (몇 가지 중요한 질문들)
1. 예측 변수 중 적어도 하나가 응답을 예측하는 데 유용한가?
2. 모든 예측 변수가 Y를 설명하는데 도움이 되는가, 아니면 예측 변수의 일부만 유용한가?
3. 모델이 데이터를 얼마나 잘 맞추는가?
4. 주어진 예측 변수 값들에 대해, 어떤 응답 값을 예측해야 하는가, 그리고 우리의 예측이 얼마나 정확한가?
1. 예측 변수 중 적어도 하나가 응답을 예측하는 데 유용한가?
우리가 단순 선형 회귀에서 예측 변수가 응답을 예측하는지 유용한지 살펴보는 방법은 H0 : B1 = 0, HA : B1 /= 0 이렇게 놓고 t검정을 하는 방법이 있었다. 그렇지만 이제는 여러 개를 비교해야 하므로 모든 회귀 계수가 0인지 확인하는 과정을 거친다.
이거는 당연하게도 ANOVA(분산 분석, 3개 이상의 평균이 같은지 확인하는 방법)을 사용하고

이런 식으로 귀무가설을 설정하고 F-통계량을 계산함으로써 이루어진다. 여기서 HA를 간과할 수 있는데 "적어도 하나의 Bn이 0이 아니다"이다.

그리고 F-statistic의 식은

F-통계량은 예측 변수들과 응답 사이에 관계가 있는지를 판단하는 데 사용된다. 만약 귀무가설이 참이라면, F-통계량은 1에 가깝게 나오며, 대립 가설이 참이라면 F-통계량은 1보다 크게 나온다.
개별 변수에 대한 p-값이 매우 작다면, 그 예측 변수는 응답과 관련이 있다고 보는 것이 일반적이지만 이런 추론은 특히 예측 변수의 수 p가 많을 때 잘못될 수 있다. ( 다중 공선성 이야기하는 것 같은데)
그리고 우리가 당연하게도 여러 개의 변수가 있을 때 일부를 뽑아서 접목시키고 싶을 때가 있는데

이 역시 위와 비슷하게 사용한다.

왜 t-test를 여러 번 하지 않을까? t-test를 여러 번하면, 우리 test의 정확도에 문제가 생긴다. 우리는 유의 수준을 보통 0.05로 잡는데, 이는 95%의 정확도를 기반에 하고 있다. 근데 정확도가 95%인 test를 여러 번 시행한다고 하면, 결국 우리의 test의 결과는 "모두 정확한 test라고 해도 (0.95)^n이라는 숫자가 되고, 5번만 수행해도 77%에 근사하는 정확도를 얻는다.
30번 정도 수행하면 적어도 한번 오류가 있을 확률이 80%까지 치솟게 된다. 따라서 여러 번 test를 하는 것은 좋지 못하다.
그리고, 예측해야 할 계수가 우리가 가진 데이터의 차원보다 많으면 (p> n)인 경우 분석이 어렵다. 이게 예시가 유전자 분석이 있다고 했다. 사람은 얼마 없는데, 분석할 유전 데이터 변수는 수억 개.. 이렇게 생각하는 게 맞나 싶다.
이러한 상황에서는 전진 선택법과 같은 다른 방법들이 사용될 수 있다.
전진 선택법(Forward Selection)은 통계적 모델링에서 사용되는 변수 선택 방법 중 하나입니다. 이 방법은 변수 선택 과정을 시작할 때 모든 독립 변수가 제외된 상태에서 시작합니다. 그리고 반복적인 과정을 거쳐 가장 유의미한 변수부터 하나씩 모델에 추가합니다. 이 과정은 미리 정의된 기준에 따라 멈춥니다. 예를 들어, 추가된 모든 변수가 통계적으로 유의미하거나, 모델의 예측 성능이 더 이상 향상되지 않을 때 멈출 수 있습니다.
전진 선택법의 단계는 다음과 같습니다:
- 먼저, 독립 변수가 없는 모델 (즉, 상수항만 있는 모델)을 설정합니다.
- 각 독립 변수를 차례대로 추가하여 모델을 만들고, 이 모델들 중에서 가장 좋은 모델 (즉, 가장 낮은 AIC, BIC 또는 가장 높은 adjusted R-squared 등의 기준을 사용)을 선택합니다.
- 이렇게 선택된 모델에 또 다른 독립 변수를 추가하여 새로운 모델들을 만들고, 이 중에서 가장 좋은 모델을 선택합니다.
- 이 과정을 더 이상 변수를 추가할 수 없거나, 더 이상 모델의 성능이 향상되지 않을 때까지 반복합니다.
전진 선택법은 계산 부담이 비교적 적으며, 큰 데이터셋에 적합합니다. 하지만 이 방법은 상호작용(interaction) 효과나 다중공선성(multicollinearity) 등의 문제를 고려하지 않기 때문에 주의가 필요합니다.
2. 모든 예측 변수가 Y를 설명하는데 도움이 되는가, 아니면 예측 변수의 일부만 유용한가?
뭐 사실상 제일 중요한 부분이 아닌가 싶다. 거의 모든 회귀분석이 일부의 데이터만 관계가 있는 경우가 있지 않을까?
일단 당연하게도 먼저 F-statistic을 계산하고, p-value를 찾는 것에 관심이 있는데, 이게 p-value가 늘어날수록, 문제가 생긴다.
그래서 현실적으로 변수 선택을 해야 하는데,
예를 들어, 만약 p가 2라면, 우리는 네 가지 모델을 고려할 수 있다 :
(1) 변수를 포함하지 않는 모델 (2) X1만을 포함하는 모델, (3) X2만을 포함하는 모델, 그리고 (4) X1과 X2 모두를 포함하는 모델.
그런 다음 우리는 고려된 모든 모델 중에서 최상의 모델을 선택해야 하는데, Mallow’s Cp, Akaike information criterion (AIC), Bayesian information criterion (BIC), and adjusted R2를 사용한다. 이건 6장에서 다시 다룬다고 하니까 참고하자
근데 이 모델들도 변수들이 너무 많아지면 고려할게 너무 많아져서 (2^p개) 잘 사용하지 않게 된다고 한다.
그래서
1. 전진 선택
이 방법은 처음에는 모델에 어떠한 변수도 포함시키지 않는다. 그다음에 각 단계에서, 모델에 아직 포함되지 않은 변수 중에서 가장 유의미한 것을 선택하여 모델에 추가하고, 이 과정을 원하는 개수의 변수가 선택될 때까지, 또는 더 이상 추가할 유의미한 변수가 없을 때까지 반복한다.
예시: p개의 예측 변수가 있을 때, 전진 선택은 다음과 같이 진행된다.
1단계: p개의 단순 선형 회귀 모델을 적합시키고, 가장 낮은 RSS 또는 가장 높은 R² 를 가진 모델을 선택한다.
2단계: 다음으로, p-1개의 변수 중 하나를 이미 선택된 변수에 추가하여 만들 수 있는 모델을 적합시킨다. 이 중에서 가장 낮은 RSS 또는 가장 높은 R²를 가진 모델을 선택한다.
그리고 위의 단계를 계속 반복한다.
2. 후진 선택
이 방법은 전진 선택과는 반대로, 처음에는 모든 변수를 모델에 포함시킨 다음에 시작한다. 그다음에 각 단계에서, 모델에서 가장 덜 중요한 변수를 제거하고, 이 과정을 원하는 개수의 변수가 남을 때까지, 또는 더 이상 제거할 덜 중요한 변수가 없을 때까지 반복한다.
예시: p개의 예측 변수가 있을 때, 후진 제거는 다음과 같이 진행된다.
1단계: 모든 변수를 포함하는 모델을 적합시킨다
2단계: p개의 변수 중 가장 중요하지 않은 변수를 찾아 제거한다.
이 과정을 반복하여 최종 모델을 선택한다.
3. 혼합 선택
이 방법은 전진 선택과 후진 제거를 결합한 방법이다. 처음에는 변수를 선택하지 않고 시작하며, 각 단계에서 가장 중요한 변수를 추가합니다. 그러나 모든 단계에서 모델의 중요성을 평가하고, 어떤 변수가 중요하지 않다면 그 변수를 제거한다. 이 방법은 전진 선택과 후진 제거의 장점을 모두 결합한 방법이다.
예시: p개의 예측 변수가 있을 때, 혼합 선택은 다음과 같이 진행된다.
1단계: p개의 단순 선형 회귀 모델을 적합시키고, 가장 낮은 RSS 또는 가장 높은 R² 를 가진 모델을 선택한다.
2단계: p-1개의 변수 중 하나를 이미 선택된 변수에 추가하여 만들 수 있는 모델을 적합시킵니다. 이 중에서 가장 낮은 RSS 또는 가장 높은 R²를 가진 모델을 선택한다.
3단계: 이제 모델에 포함된 각 변수의 중요성을 평가한다.. 만약 중요하지 않은 변수가 있으면 그 변수를 제거한다.
이 과정을 반복하여 최종 모델을 선택한다.
이렇게 3가지 방식을 사용한다고 적혀있다.
이러한 방법들은 모델의 복잡성과 적합도 사이의 균형을 찾는 데 도움을 줍니다. 너무 많은 변수를 포함하는 모델은 오버피팅의 위험이 있으며, 반면에 너무 적은 변수를 포함하는 모델은 응답 변수의 변동을 충분히 설명하지 못할 수 있습니다. 이러한 방법들은 이 두 가지 극단 사이의 적절한 균형을 찾는 데 도움을 줍니다.
3. 모델이 데이터를 얼마나 잘 맞추는가? (예측)
모델 적합도를 가장 흔하게 측정하는 두 가지 수치적 방법은 잔차 제곱합(RSE)과 결정계수(R²)인데, 이는 설명된 분산의 비율이다.
그니까 이게 RSE는 예측값과 실제값이 얼마나 차이가 나냐를 보는 값인데 이는 예측값과 실제값이 얼마나 떨어져 있냐로 이야기할 수 있어서 분산으로 이해될 수 있고, 결정계수는 모델이 데이터의 분산을 얼마나 잘 설명하고 있냐를 나타내는 척도이기 때문에 설명된 분산이라고 할 수 있다. 예를 들어, R²가 0.9라면, 모델이 관측된 데이터 분산의 90%를 설명하고 있다는 것이다.
따라서, '설명된 분산의 비율'이라는 말은 모델이 데이터의 분산, 즉 데이터가 얼마나 퍼져 있는지를 얼마나 잘 설명하고 있는지를 나타내는 척도입니다. 이는 결국 모델이 데이터를 얼마나 잘 '이해'하고 있는지를 나타내는 지표라고 할 수 있습니다.
이들 수량은 단순 선형 회귀에서와 같은 방식으로 계산되고 해석된다.
단순 회귀에서, R²는 응답과 변수의 상관관계의 제곱이다. 다중 선형 회귀에서는 Cor(Y, Yˆ ) ², 즉 응답과 적합된 선형 모델 간의 상관관계의 제곱과 동일하다는 것이 밝혀졌다. 사실, 적합된 선형 모델의 한 가지 특성은 가능한 모든 선형 모델 중에서 이 상관관계를 최대화한다는 것이다.
R² 값이 1에 가까울수록 모델이 응답 변수의 분산을 많이 설명한다는 것을 나타낸다. 예를 들어, 광고 데이터에서 모든 세 가지 광고 매체를 사용하여 판매를 예측하는 모델의 R²가 0.8972 임을 확인했다. 반면에 TV와 라디오만을 사용하여 판매를 예측하는 모델의 R² 값은 0.89719다. 즉, TV와 라디오 광고가 이미 포함된 모델에 신문 광고를 포함하면 R²가 약간 증가하며, 이전에 신문 광고의 p-값이 유의하지 않다는 것을 확인했다.
R²는 응답과 약하게만 연관된 변수를 모델에 추가하더라도 항상 증가한다는 것이 밝혀졌다. 이는 또 다른 변수를 추가하면 항상 훈련 데이터의 잔차 제곱합이 감소하기 때문이다(비록 테스트 데이터는 반드시 그런 것은 아니다). 따라서 훈련 데이터에서도 계산되는 R² 통계량은 반드시 증가해야 한다. TV와 라디오 광고만을 포함하는 모델에 신문 광고를 추가하면 R²가 아주 조금 증가하는 사실은 신문을 모델에서 제외할 수 있는 추가적인 증거를 제공한다. 본질적으로, 신문은 훈련 샘플에 대한 모델 적합도를 실제로 향상하지 않으며, 그 포함은 과적합으로 인해 독립 테스트 샘플에서 나쁜 결과를 초래할 가능성이 있다.
그냥 요약하고 정리하다가 생각난 건데 이거 생각보다 유익함 근데 설명이 너무 상세해서 어디까지 끊어서 적어야 하는지 모르겠어..
RSE와 R² 통계량을 살펴보는 것 외에도 데이터를 그래프로 표현하는 것이 유용할 수 있다. 그래픽 요약은 숫자 통계에서는 보이지 않는 모델의 문제를 드러낼 수 있다

예를 들어, 그림 3.5는 TV와 라디오에 대한 판매의 3차원 플롯을 보여준다. 일부 관찰은 최소 제곱 회귀 평면 위에, 일부는 아래에 위치한다는 것을 볼 수 있다.
4. 주어진 예측 변수 값들에 대해, 어떤 응답 값을 예측해야 하는가, 그리고 우리의 예측이 얼마나 정확한가?
이는 신뢰구간을 사용하고, 모델을 완성해도 잠재적으로 축소 가능 오차라는 원인이 있는데, 말 그대로 실제 데이터는 선형이 아닌데 선형을 가정하고 모델을 사용하기 때문에 발생하는 오차이다. 그리고 당연하게 랜덤 한 오차가 존재해서 Irreducible error 즉, 줄일 수 없는 에러는 존재한다. 그래서 예측 구간을 사용하게 된다.
3.3 Other Considerations in the Regression Model
3.3.1 Qualitative Predictors
양적변수만 있어서 쉬웠지? 하하 질적인 변수를 만나면 상관관계를 찾을 수 없다.
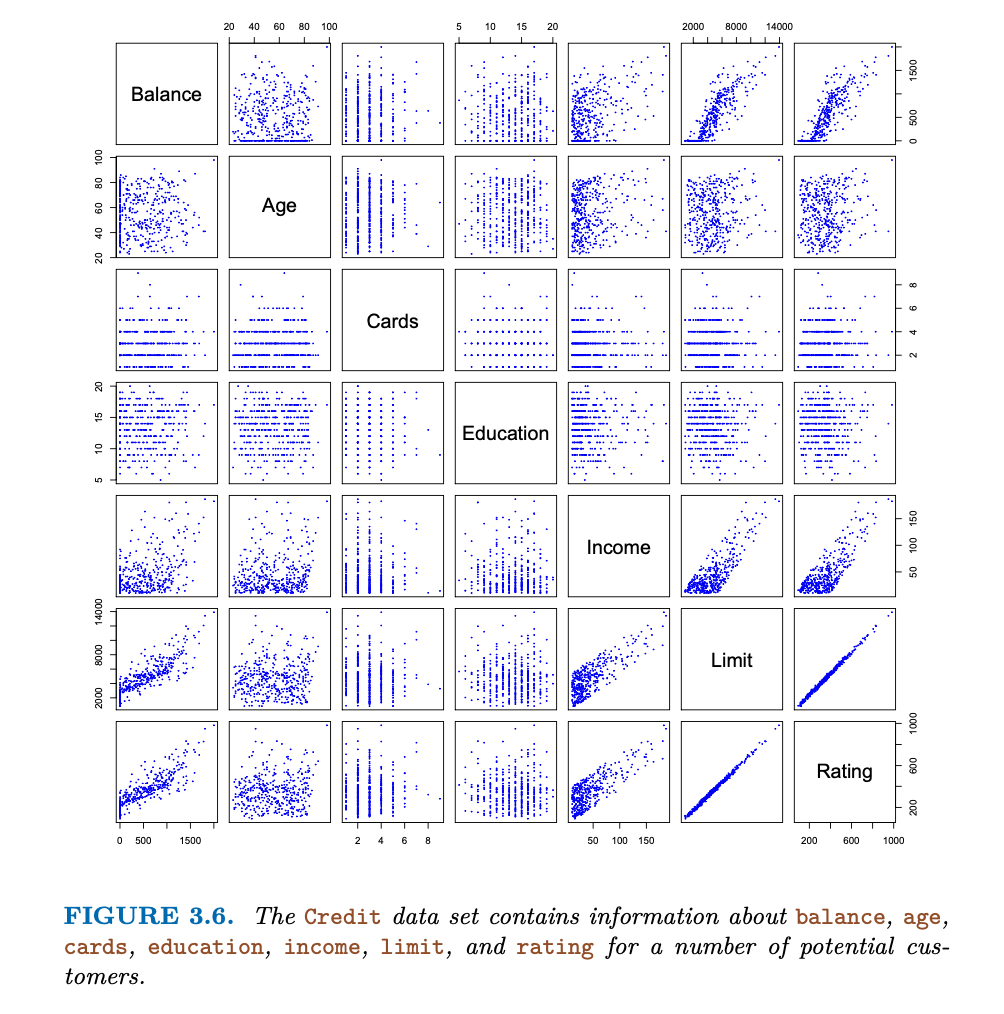
예를 들어, 신용 카드 잔액, 나이, 카드 수, 교육 기간, 소득, 신용 한도, 신용 등급과 같은 양적 예측 변수 외에도 집 소유, 학생 상태, 혼인 상태, 지역 등의 질적 변수가 있다.
Predictors with Only Two Levels (A or B만 가진 것을 이야기한다.)
범주형 데이터가 두 개의 수준만을 가지고 있는 경우 단순하게 더미화 한 후에 값을 처리하면 좋다. 그러니까 이런 식으로

변경해서 사용한다.
Qualitative Predictors with More than Two Levels (2가지 이상을 가진 경우)

2가지 이상을 가지는 경우 이런식으로 각각 조건에 따라 생성해 준다.
(여기서 보면 3개일 때 2개, n개 일 때 n-1개의 더미변수가 생길 수 있다.라고는 나와있는데 맞지 않을까..?)
3.3.2 Extensions of the Linear Model
선형 회귀 모델은 유연성이 제한되어 있다는 큰 단점이 있다. 그니까 이 놈 시키 직선 밖에 못 그어. 박 씨!
특히, 선형 회귀는 예측 변수와 응답 사이의 관계가 선형이라고 가정하는데, 상식선에서 생각해도 이 가정이 실제로 충족되는 경우는 드물다.
Removing the Additive Assumption ( 첨가 가정의 제거)
말이 진짜 뭣 같다, 이래서 해석본 안 사나
"Additive Assumption"이란, 서로 다른 요소들이 독립적으로 작동하며, 각 요소의 효과가 서로를 방해하지 않고 단순히 합산되는 것이라고 가정하는 것이다. 예를 들어, 아이스크림 가게에서 매출을 늘리는 두 가지 방법이 있다고 생각해 보자 : 아이스크림의 맛을 향상하는 것과 가게의 위치를 좋은 곳으로 바꾸는 것이 있다고 생각하자.
"Additive Assumption"에 따르면, 이 두 가지 방법은 각각 독립적으로 작동하며, 그 효과는 단순히 더해진다. 다른 이야기로 하면 서로 영향을 받지 않는 독립이라는 것이다. 즉, 아이스크림 맛을 향상하면 매출이 30% 증가하고, 가게 위치를 좋은 곳으로 바꾸면 매출이 추가로 20% 증가하여, 두 방법을 모두 사용하면 매출은 총 50% (30% + 20%) 증가한다는 것이다.
그러나 이런 가정은 항상 정확할 수가 있나. 당연히 서로 상호작용을 해서 둘 다면 효과가 극대화될 것이다. 따라서 "Additive Assumption"을 제거한다는 것은, 서로 다른 요소들이 상호작용할 수 있고 그 효과가 단순히 더해지지 않을 수 있다는 것을 인정하는 것이다.
다시 아이스크림 가게 예시로 돌아가보면, 아이스크림의 맛을 향상하고 가게 위치를 좋은 곳으로 바꾸는 것이 서로 상호작용할 수 있다. 아이스크림의 맛이 좋아지면 사람들이 더 많이 찾아올 것이고, 그와 함께 가게 위치가 좋아지면 그 효과는 더욱 커질 것이다. 이러한 상호작용을 고려하면, 두 가지 방법을 동시에 사용하면 매출은 50% 이상 증가할 수 있다는 것을 알 수 있다.
그니까 우리는 위에서 계속 변수들이 서로 독립이라고 하고 선형회귀식을 사용했는데 당연히 이게 문제가 되는 거지 뭐, 그래서 그 가정을 제거해 준다는 뜻이다. => 그러면 사실 내가 준 통계에서는 아무것도 쓸 수 있는 게 없음... (내가 알기로는?)

이랬던 식이

이런 식으로 변결될 수 있다는 것이다.
Non-linearity of the Data

당연히 예측 변수와 실제값의 관계가 비선형일 수 있다.
선형 회귀 모델은 응답과 예측 변수 간의 선형 관계를 가정하지만, 실제로는 비선형 관계가 있을 수 있다. 이러한 비선형 관계를 포착하기 위한 한 가지 방법은 다항 회귀를 사용하는 것이다. 이는 예측 변수의 변형된 버전을 모델에 포함시킴으로써 선형 모델을 비선형 관계에 적응시키는 방법이다.
3.3.3 Potential Problems
1. Non-linearity of the Data
설명 변수를 log, sqrt, 제곱 등을 취해 비선형적으로 변환하여 회귀모델에 적용하는 것이 방법.
In the later chapters of this book, we will discuss other more advanced non-linear approaches for addressing this issue.
2. Correlation of Error Terms
실제로 오차 항목들 사이에 상관성이 있다면, 추정된 표준 오차는 실제 표준 오차를 과소평가하게 될 것입니다. 결과적으로, 신뢰 구간과 예측 구간은 실제보다 좁게 나타날 것이며, 95% 신뢰 구간이 실제로는 매개변수의 참값을 포함할 확률이 0.95보다 훨씬 낮게 될 수 있습니다. 또한, 모델과 관련된 p-값도 실제보다 낮게 나타나, 이로 인해 우리는 통계적으로 유의한 매개변수로 잘못 판단할 수 있습니다. 간단히 말해서, 오차 항목들이 상관성을 가지면, 우리의 모델에 대한 과도한 자신감을 가질 수 있습니다.
이러한 오차 항목들 사이의 상관성이 나타나는 이유는 무엇일까요? 이러한 상관성은 대개 시계열 데이터에서 자주 발생합니다. 시계열 데이터란 시간의 이산적인 지점에서 측정된 관측값들로 구성됩니다. 많은 경우에, 인접한 시점에서 얻은 관측값들은 긍정적으로 상관된 오차를 가지게 됩니다. 이를 확인하기 위해, 우리는 모델의 잔차를 시간 함수로 그려볼 수 있습니다.
만약 오차가 상관성이 없다면, 잔차에서는 분명한 패턴이 나타나지 않아야 합니다. 반면에, 오차 항목들이 긍정적으로 상관되어 있다면, 잔차에서는 추적이 나타나게 됩니다. 즉, 인접한 잔차는 비슷한 값을 가지게 됩니다.
시계열 데이터에서의 오차 항목들 사이의 상관성을 적절하게 처리하기 위한 많은 방법들이 개발되어 왔습니다. 또한, 시계열 데이터 외에도 오차 항목들 사이의 상관성이 나타날 수 있습니다. 예를 들어, 체중으로부터 개인의 신장을 예측하는 연구를 생각해 봅시다. 오차 항목들이 상관성이 없다는 가정은 연구 대상자들 중 일부가 같은 가족이거나, 같은 식단을 섭취하거나, 같은 환경 요인에 노출되었다면 위반될 수 있습니다.
일반적으로, 오차 항목들이 상호 상관성이 없다는 가정은 선형 회귀뿐만 아니라 다른 통계적 방법들에 있어서도 매우 중요하며, 이러한 상관성의 위험을 줄이기 위해서는 좋은 실험 설계가 중요하다는 결론을 내릴 수 있습니다.

3. Non-constant Variance of Error Terms (특이값)
4. Outliers
5. High Leverage Points (고지렛점... 와우 용어 그냥 죽었다높은 레버리지를 가진 포인트)
"High Leverage Points"라는 개념을 설명하기 위해, 우리가 집을 팔려고 한다고 가정해 볼게요. 그런데 집의 가격을 결정하는 데 어떤 요소들이 중요할까요? 집의 크기, 위치, 방의 수 등 여러 가지가 있겠죠.
선형 회귀 모델을 사용하면, 이런 요소들이 집의 가격에 얼마나 영향을 미치는지 알 수 있습니다. 이때, 대부분의 집들은 가격을 예측하는 데 도움이 되지만, 몇몇 집들은 다른 집들과 매우 다른 특성을 가질 수 있습니다. 예를 들어, 아주 크거나 작은 집, 아주 좋거나 나쁜 위치에 있는 집 등이 있겠죠.
이런 집들을 "High Leverage Points"라고 부릅니다. 왜냐하면 이런 집들은 모델이 집의 가격을 어떻게 예측하는지에 큰 영향을 미치기 때문이죠. 그래서 이런 "High Leverage Points"를 발견하면, 그 집들이 왜 다른 집들과 다른지를 파악하고, 그 영향이 우리의 예측에 어떤 영향을 미치는지를 이해하는 것이 중요합니다.
6. Collinearity (공선성)


"Collinearity" 또는 "다중공선성"은 통계학과 머신러닝에서 자주 다루는 주제이다. 이는 여러 설명 변수(predictor variables 또는 features)가 서로 강하게 상관관계가 있을 때 발생하는 문제를 의미한다.
예를 들어, 집 값을 예측하기 위해 집의 크기와 방의 수를 변수로 사용한다고 가정해 보면, 집의 크기가 클수록 방의 수도 많을 것이므로, 이 두 변수는 서로 강하게 연관되어 있을 가능성이 높습니다. 이러한 상황을 다중공선성이라고 한다.
다중공선성이 발생하면, 다음과 같은 문제가 발생할 수 있다 :
- 회귀 계수 추정치가 불안정해집니다: 즉, 작은 데이터 변화에도 불구하고 계수 추정치가 크게 변할 수 있습니다.
- 회귀 계수의 해석이 어려워집니다: 예를 들어, 한 변수의 효과를 다른 변수의 효과와 분리하여 이해하는 것이 어렵습니다.
- 불필요하게 복잡한 모델을 만들 수 있습니다: 예를 들어, 실제로는 필요하지 않은 변수가 모델에 포함될 수 있습니다.
다중 공선성을 해결하는 방법에는 변수 선택(특정 변수 제거), 차원 축소, 정규화(regularization) 등이 있다. 이 방법들은 모두 공선성이 있는 변수들 사이의 관계를 줄이거나 모델의 복잡성을 줄이는 데 목표를 두고 있다.
3.4 The Marketing Plan
그래서 이 장에서는 다시 처음의 질문으로 돌아간다
1. 광고 예산과 판매량의 상관관계가 있는가?
다중 회귀 모델을 사용해서 상관관계를 확인할 수 있었다.

2. 얼마나(How strong) 그 둘의 사이가 관계 있는지
첫째, RSE는 응답의 표준 편차를 모집단 회귀선에서 추정합니다. 광고 데이터의 경우 RSE는 1.69 단위이며 응답의 평균값은 14.022로, 대략 12%의 오차율을 나타냅니다. 둘째, R^2 통계량은 예측 변수로 설명되는 응답의 변동성 비율을 기록합니다. 예측 변수들은 판매량의 분산의 거의 90%를 설명합니다
3. (광고의 플랫폼) 미디어와 판매량이 관계가 있는지

다중 선형 회귀에서 TV와 라디오의 p-value는 낮지만 신문의 p-value는 그렇지 않습니다.
TV와 라디오만이 판매량과 관련이 있음을 나타낸다. (6장에서 자세히 나와있습니다.)
4. 그 둘의 사이가 얼마나 상관관계가 있는지
- 광고 데이터를 통해 TV, 라디오, 신문의 계수에 대한 95% 신뢰 구간을 계산했다. TV와 라디오의 신뢰 구간은 0에서 멀며 좁아 판매와 관련이 있다는 증거가 되지만, 신문의 신뢰 구간은 0을 포함하여 통계적으로 유의하지 않다.
- 다중공선성은 표준 오차를 매우 크게 만들 수 있다. 그러나 TV, 라디오, 신문의 VIF 점수는 다중공선성의 증거를 보이지 않는다.
- 각 매체가 판매량에 미치는 영향을 평가하기 위해 세 개의 단순 선형 회귀를 수행할 수 있다. TV와 라디오는 판매량과 매우 강한 연관이 있고, 신문은 약한 연관이 있다.
5. 미래 판매 예측량을 얼마인지
- 응답은 (3.21)을 사용하여 예측될 수 있다.
- 예측의 정확도는 개별 응답을 예측하느냐, 아니면 평균 응답을 예측하느냐에 따라 다르다. 전자의 경우 예측 구간을, 후자의 경우 신뢰 구간을 사용한다. 예측 구간은 항상 신뢰 구간보다 넓다.
6. 이게 선형관계인지?
- 잔차 그래프를 사용하여 비선형성을 식별할 수 있다.
- 관계가 선형이면 잔차 그래프에는 어떠한 패턴도 나타나지 않아야 한다.
- 광고 데이터에서는 비선형 효과를 관찰했으며, 이는 잔차 그래프에서도 관찰될 수 있다.
7. 미디어 광고 간의 시너지가 있는지
덧셈 ( 아마 시너지 관계라고 생각하면 될 듯) 관계를 가정하고 하는데, 예측 변수들이 독립이기 때문에 비현실적일 수 있다.
여기서는 상호작용을 가진 항이 있다는 것을 P-vlaue로 확인 할 수 있고, 상호작용이 포함된 모델을 만들면 R^2값이 90%에서 97%까지 증가한다.
3.5 Comparison of Linear Regression with K-Nearest Neighbors (선형 회귀 분석과 K-근접 이웃 비교)
linear regression은 f(x)가 선형이라고 가정하고 수행하는 모수적(parametric) 방법이다.
cf) 모수적 방법과 비모수적 방법은 말 그대로 "모수"를 가정하고 실험을 진행하는지 모수를 가정하지 않고 진행하는지에 따라 나눈다. 이미 linear regression은 모수가 선형 관계라는 것을 가정하고 진행하기 때문에 모수적 방법으로 분류된다.
모수적 방법은 1. often easy to fit 2. the coefficients have simple interpretations (계수들의 간단한 해석) 3. tests of statistical significance can be easily performed (통계적 유의성 검정도 쉽게 수행가능)
단점이 당연하게도 식의 형태를 정해 놓고 들어가는 방법이기 때문에, 식이 내가 지정한 함수를 벗어나는 경우 성능이 많이 떨어집니다.
반면에, 비모수적 방법 (non-parametric)은 정확히 식을 정해놓고 들어가는 방식이 아니기 때문에, 회귀를 수행하는데 있어 유연한 접근을 할 수 있는 방법을 줍니다.
여기서는 모수적 방법인 선형회귀 대신 비 모수적 방법인 K-NN regression(K-Nearest neighbors regression)을 제시합니다.
그냥 가까이 있는 K개의 데이터에 기대서 내가 어디 속하는지 추정하는 방법입니다.
K 값과 예측 점 x0가 주어지면, KNN 회귀는 먼저 x0에 가장 가까운 K개의 학습 관측치를 식별하며, 이를 N0로 표현합니다. 그런 다음 N0의 모든 학습 응답의 평균을 사용하여 f(z)를 추정합니다.
즉,

이와 같은 식으로 표현될 수 있습니다.

그림 3.16은
p=2 예측 변수를 가진 데이터 세트에서 두 KNN 적합을 보여줍니다. K = 1인 적합은 왼쪽 패널에 표시되며, 오른쪽 패널은 K = 9에 해당합니다. K = 1일 때 KNN 적합은 학습 관측치를 완벽하게 보간하며, 따라서 계단 함수의 형태를 취합니다. K = 9일 때 KNN 적합은 여전히 계단 함수이지만, 9개의 관측치에 대한 평균을 내면 상수 예측의 영역이 훨씬 작아져 더 부드러운 적합이 됩니다. 일반적으로, K의 최적 값은 2장에서 소개한 편향-분산 트레이드오프에 따라 달라집니다. K의 작은 값은 가장 유연한 적합을 제공하며, 편향은 낮지만 분산은 높습니다. 이 분산은 주어진 영역에서의 예측이 단 하나의 관측치에 완전히 의존하기 때문입니다.
그러면 비모수적 방법과 모수적 방법 중에 뭐가 더 우수 할까?
당연히 정답은 : 우리가 모수적 방법에서 가정한 함수 f(x)에 가까울 수록 모수적 방법이 우수하다.


위의 그래프들은 관계가 선형이면 선형 회귀가 성능이 약간 더 좋고, 관계가 비 선형이면 K-NN이 더 성능이 좋은 것을 보여주고 있습니다.

When p = 1 or p = 2, KNN outperforms linear regression. But for p = 3 the results are mixed, and for p ≥ 4 linear regression is superior to KNN.
판단 기준 자체는 MSE(Mean Square Error)입니다. => KNN은 차원이 증가할 수록 성능이 감소하는 문제가 있음
p : 차원수
p = 1일 때, 이것은 f(X)를 정확하게 추정하기에 충분한 정보를 제공하지만 p = 20개의 차원에 걸쳐 50개의 관측치를 확산하면 주어진 관측치에 인접한 이웃이 없는 현상이 발생하는데, 이는 차원의 저주라고 합니다.
즉, p가 클 때 주어진 테스트 관측치 x0에 가장 가까운 K 관측치는 p 차원 공간에서 x0으로부터 매우 멀리 떨어져 f(x0)에 대한 예측을 매우 나쁘게 할 수 있으며, 따라서 KNN 적합도가 좋지 않습니다.
일반적으로, 모수적 방법은 예측 변수당 관측치의 수가 적을 때 비모수적 접근법보다 성능이 우수한 경향이 있습니다.
'미래내일일경험 - 빅리더(23.06~23.12) > 교육' 카테고리의 다른 글
| [An Introduction to Statistical Learning] 3. Linear Regression_Exercise (0) | 2023.08.12 |
|---|---|
| [스터디챌린지] ICT융합대학 스터디 챌린지 6주차(8/05 ~ 8/11) (1) | 2023.08.11 |
| [스터디챌린지] ICT융합대학 스터디 챌린지 5주차(7/29 ~ 8/04) (0) | 2023.08.04 |
| [파이썬] 리스트, 딕셔너리 시간 복잡도 체감하기 (1) | 2023.07.28 |
| [스터디챌린지] ICT융합대학 스터디 챌린지 4주차(7/22 ~ 7/28) (0) | 2023.07.27 |