Classification 모델의 평가하는 지표를 설명하면서 CAP Curve가 나왔는데,
ROC Curve랑 축을 제외하고 비슷해서 정리하기 위해서 작성한다.
1. CAP (Cumulative Accuracy Profile) Curve
"누적" 정확도 프로파일 곡선
CAP Curve를 알아보려면, 나온 맥락부터 알아야한다. Confusion matrix부터 살펴보자.
| 예측 데이터 | |||
| True | False | ||
| 실제 데이터 | True | Ture Positive | False Negative |
| False | False Positive | Ture Negative | |
다들 알고 있는 내용일 것이다. Classfication 문제에서 모델의 성능을 측정하기 위해서 사용한다.
여기서 살펴보야아 할 것은 Type1, Type2 Erorr이다.
Type 1 Error : False Positive
Type 2 Error : False Negative
보통 모델을 설계한 입장에서 조금 더 치명적인 오류는 Type 2 Error다.
암으로 예시를 들어보면 Type 1 Error는 암이 없는데 암이 있다고 모델이 잡은 경우이다.
항암치료를 한다고 해도 환자에게 그렇게 크리티컬 하지 않을 것이다.
문제는 Type 2 Error다. 암이 있는데, 암이 없다고 모델이 잡아버리면.. 암은 더욱 진행 될 것이다.
그래서 보통 우리는 Type 2 Error를 최대한 줄이는데 포커스를 맞춰서 진행한다. (도메인이나 데이터마다 다르지만 보통 그런다.)
여기서 모델의 평가지표를 '정확도'로 설정하면 문제가 발생한다.
그걸 우리는 Accuracy Paradox (정확도 역설)라고 부른다. 밑의 예시를 보자. 숫자로 이해하면 더 편한다.
| 예측 데이터 | |||
| True | False | ||
| 실제 데이터 | True | 100 | 50 |
| False | 150 | 9700 | |
이 경우에는 정확도는 97%이고, 2종 오류의 수는 50이다.
(Accuracy = 9,700 / 10,000 = 97%)
하지만, 아래 경우로 결과가 바뀌는 경우
| 예측 데이터 | |||
| True | False | ||
| 실제 데이터 | True | 0 | 150 |
| False | 0 |
9850 | |
정확도가 98.5%로 오르지만, 2종 오류는? 3배나 많아진 150이다.
(Accuracy = 9,850 / 10,000 = 98.5%)
치명적인 오류는 3배나 늘어났지만, 정확도는 높아져서 좋은 모델이라 평가해버린다.
그래서 우리는 이럴 때, Cumulative Accuracy Profile Curve를 사용한다.
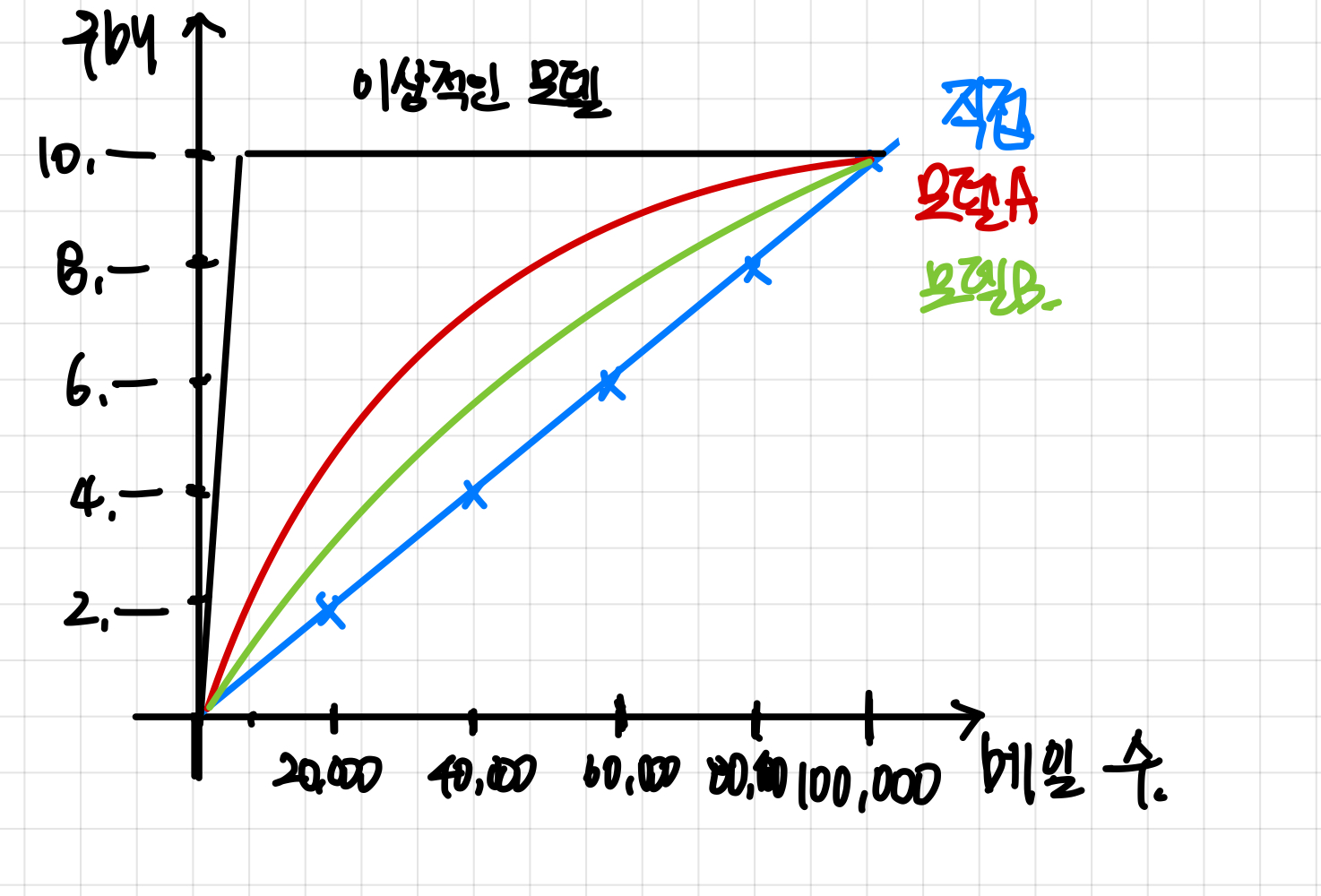
아무런 정보 없이 메일을 하나하나 직접 보냈을 때,
파란선의 그래프가 나온다고 하자, 100,000개의 메일을 보내면, 10,000명이 우리의 제품을 구매한다.
만약 구매 할 고객을 예측하는 모델을 하나 만들어서 그 모델에서 구매할 것이라고 나온 고객에게 메일을 보낸다고 하자, 우리 제품을 구매할 고객은 총 10,000만명인데, 아무 사전 정보 없이 메일을 보냈던 파란 그래프와는 다르게,

보다 적은 메일수로 많은 구매를 일으킨다. (모델 A는 7,000명 정도가, 모델 B는 5,500명 정도가 구매한 것을 볼 수 있다.)
여기서 Accuracy ratio를 뽑을 수 있다.

Accuracy ratio = A / (A + B)
그리고 수치적인 평가는 메일 수의 50%의 구간에서 구매를 X%하는지로 평가할 수 있다.
| X < 60% | 매우 안좋음 |
| 60% <= X < 70% | 평균 |
| 70% <= X < 80% | 좋음 |
| 80% <= X < 90% | 매우 좋음 |
| 90% <= | 완벽함 |
더 좋은 모델을 오류 없이 고를 수 있다.
(적어도 Accuracy Ratio는 피할 수 있다.)
2. ROC (Receiver Operating Characteristic) Curve
특이도가 변할 때, 민감도가 어떻게 변하는지 나타내는 곡선
특이도 : 실제 Negative인 것 중 Negative로 예측한 값의 비율
민감도 (Recall, 재현율) 실제 Posivite인 것 중 Positive로 예측한 값의 비율
Y축은 1 - 특이도, X축은 민감도로 구성됨.
왼쪽 상단에 가까울 수록 좋은 모델을 나타냄

좀 많이 똑같이 생기고, 45도 선보다 위에 있어야 성능이 좋아진다는 점. 그래프 밑의 면적을 사용한다는 점이 똑같이서 정리한다